Física 10 I.E.D. Las américas.
Área:
Ciencias naturales
|
Asignatura:
Física.
|
|
Grado:
10°
|
Periodo:
I
|
|
Docente:
Ulises De la Rosa Castrillón.
Taller
No 1.
|
Duración:
3 horas .1 semana
|
Fecha: 27 de marzo. 2020.
|
2.
PLANEACIÓN:
ESTÁNDARES: Establece relaciones
entre las diferentes fuerzas que actúan sobre los cuerpos en reposo o en
movimiento rectilíneo uniforme y establece condiciones para la conservar la
energía mecánica.
|
||
Competencia del área: Uso comprensivo del
conocimiento científico, Explicación de fenómenos e Indagación.
|
||
DBA: Comprende, que el reposo o el
movimiento rectilíneo uniforme, se presentan cuando las fuerzas aplicadas
sobre el sistema se anulan entre ellas, y que en presencia de fuerzas
resultantes no nulas se producen cambios de velocidad.
|
||
TÓPICO GENERATIVO: ¿Que significa que la aceleración de la gravedad es
de 9,8 m/s2 hacia abajo?
|
||
TÓPICO: Conceptos de
cinemática. 1.- Movimiento de caída libre. 2.- Solución de problemas
|
||
META DE
COMPRENSIÓN: Los
estudiantes comprenderán cómo resolver problemas de movimiento rectilíneo,
caída libre, magnitudes vectoriales y movimiento de proyectiles, así como las
características de estos tipos de movimiento.
|
||
Desempeños de
comprensión
|
Valoración Continua (formativa)
|
Materiales y Recurso
|
DESEMPEÑO INICIAL: (Conocimientos
Previos)
Los
estudiantes responderán el siguiente cuestionario.
El estudiante responderá las siguientes preguntas:
1.- ¿Que es la rapidez media?
2.- ¿Que es el desplazamiento?
3.- ¿Que es la velocidad media?
4.- ¿Que es la aceleración?
Luego enviar al
correo que esta al final el documento con las respuestas, anotando el nombre
del estudiante.
El estudiante leerá el tópico generativo.
DESEMPEÑO
DE INVESTIGACIÓN GUIADA:
Se entregarán a los estudiantes el material
didáctico, el cual leerán y en lo posible con la ayuda de los padres
aclararán dudas recurriendo a otras fuentes como libros y sitio web
recomendado.
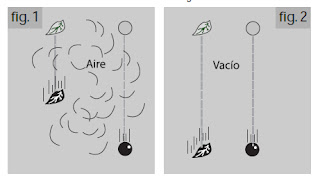
Figura B: En el vacío la piedra y la pluma caen juntas
Los cuerpos ligeros tardan más en caer a causa
de la resistencia del aire
Formulas: Movimiento vertical hacia arriba Vf =
Vo – g.t
La altura h o y,
h= Vo.t – g.t2/2.
Movimiento vertical hacia abajo Vf = Vo +
g.t y
h= Vo.t + g.t2/2.
·
La velocidad en el punto de altura
máxima es cero.
·
La rapidez de subida y la rapidez de
bajada a una misma altura es igual.
·
El tiempo que demora el proyectil en llegar al
punto más alto, es el mismo que demora en caer al suelo y se calcula con la
fórmula: Tmáx = Vo/g.
·
La altura máxima a la que llega el objeto está
dada por la fórmula:
Hmáx
o Ymáx = Vo2/ 2.g
Ejemplo: Se lanza verticalmente un objeto con
una Vo vel. Inicial de 45m/s, encuentra la altura y la velocidad de este a 3
segundos de lanzarlo y el tiempo y la altura máxima que alcanza.
Datos: Vo = 45 m/s. g = 9,8 m/s2 y t = 3 seg.
Reemplazando: Vf = 45 m/s – 9,8 m/s2
x3 seg = 45 -29,4 = 15,6 m/s, entonces: Vf = 15,6 m/s.
Calculamos la altura h = 45 m/s x 3 seg –
9,8 m/s2 x (3 seg)2/ 2 =
H= 135 m – (9,8 x9)/2 = 135m – 44,1m = 90,9 m
Tmáx = 45 m/s/9,8 m/s2 = 4,5 seg. (Tiempo en llegar a lo más alto)
Hmáx = (45 m/s)2/2x(9,8 m/s2
) = 2025 m2/ s2/19,6 m/s2. = 103,3 m (Altura
máxima que alcanza el objeto)
1.
Consultar el
tutorial de you tube para reforzar.
DESEMPEÑO
FINAL:
Actividad a desarrollar:
Taller, teniendo como base el material entregado.
Resuelve el
siguiente problema: Se lanza verticalmente un objeto con una Vo vel. Inicial de 55m/s,
encuentra la altura y la velocidad de este a 4 segundos de lanzarlo y el
tiempo y la altura máxima que alcanza.
Cualquier duda o inquietud,
enviar un mensaje al correo:
Ulisesdelarosa2010@gmail.com. Con gusto los atenderé.
Una vez terminado el taller final enviarlo a este correo. Plazo de envio de
actividades y talleres 24 de abril. 2020.
|
Con la supervisión y apoyo de los padres el
estudiante contestara el siguiente cuestionario.
Manejo del
recurso físico, textos y recursos informáticos para aclarar dudas con
el apoyo del cuidador o padres si es posible.
Comprensión de conceptos.
Se evaluará la comprensión de conceptos y la
solución de problemas.
|
Medios electrónicos,
taller, cuaderno, lápices, regla y borrador.
|
3. OBSERVACIONES:
ELABORADO POR:
|
REVISADO POR:
|
Ulises De la rosa Castrillón.
|
Área:
Ciencias naturales
|
Asignatura:
Física.
|
|
Grado:
10°
|
Periodo:
I
|
|
Docente:
Ulises De la Rosa Castrillón.
Taller
No 2.
|
Fecha: 27 de marzo. 2020.
|
|
2.
PLANEACIÓN:
ESTANDARES: Establece relaciones
entre las diferentes fuerzas que actúan sobre los cuerpos en reposo o en
movimiento rectilíneo uniforme y establece condiciones para la conservar la
energía mecánica.
|
||
Competencia del área: Uso comprensivo del
conocimiento científico, Explicación de fenómenos e Indagación.
|
||
DBA: Comprende, que el reposo o el
movimiento rectilíneo uniforme, se presentan cuando las fuerzas aplicadas
sobre el sistema se anulan entre ellas, y que en presencia de fuerzas
resultantes no nulas se producen cambios de velocidad.
|
||
TÓPICO GENERATIVO: ¿Que significa que la aceleración de la gravedad es
de 9,8 m/s2 hacia abajo?
|
||
2.- Solución de problemas.
|
||
META DE
COMPRENSIÓN: Los
estudiantes comprenderán cómo resolver problemas de movimiento rectilíneo,
caída libre, magnitudes vectoriales y movimiento de proyectiles, así como las
características de estos tipos de movimiento.
|
||
Desempeños de
comprensión
|
Valoración Continua (formativa)
|
Materiales y Recurso
|
DESEMPEÑO INICIAL: (Conocimientos
Previos)
Los estudiantes
responderán el siguiente cuestionario.
El estudiante responderá las siguientes preguntas:
Contesta V o F. (Verdadero o Falso).
En el lanzamiento vertical de un objeto hacia
arriba
1.- El tiempo de subida es menor que el tiempo de
bajada al mismo punto de partida ( )
2.- La velocidad de subida a una altura es igual a
la velocidad de bajada a esa misma altura (
)
3.- La velocidad máxima está en el punto más alto
( )
4.- La aceleración subiendo es diferente a la
aceleración bajando ( )
5.- La gravedad de un objeto cuando baja es
positiva ( ).
Luego enviar al
correo que esta al final el documento con las respuestas, anotando el nombre
del estudiante.
DESEMPEÑO DE INVESTIGACIÓN GUIADA:
Se entregarán a los estudiantes el material didáctico, el cual leerán y en lo posible con la ayuda de los padres aclararán dudas recurriendo a otras fuentes como libros y sitio web recomendado.
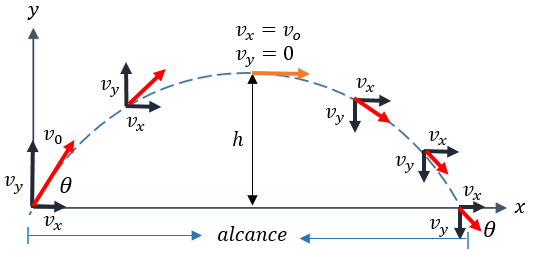
TIRO PARABÓLICO O MOVIMIENTO PARABÓLICO. Describimos el tiro parabólico mediante un sistema de coordenadas cuyo origen coincida con el punto de lanzamiento, y sus ejes vertical y horizontal determinan el plano sobre el cuál se realiza el movimiento. En la siguiente figura, representamos esta situación. Dibujamos el móvil mediante un punto negro sobre el cuál indicamos la velocidad inicial Vo. El ángulo θ que forma este vector con el eje x se denomina ángulo de lanzamiento o de tiro. Dada la independencia de los movimientos horizontal y vertical, descomponemos la velocidad inicial en sus componentes a lo largo de nuestros ejes. La composición horizontal permanecerá constante, mientras que la componente vertical variará debido a la aceleración gravitacional y tiene un valor inicial de Voy.
Un tiempo t después del lanzamiento, la velocidad
horizontal seguirá siendo Vx cuyo valor es Vo. cos θ.
El valor y el signo de la velocidad vertical esta
dado por la ecuación del movimiento vertical hacia arriba Vf = Vo –
g.t, si Vo es Voy = Vo. sen θ, reemplazamos en la fórmula.
Vf = Vo. sen θ – g.t
El valor de la posición a lo largo del eje x, dado
que el movimiento en esta dirección es rectilíneo uniforme será al cabo de
ese mismo tiempo t.
X = Vo. cos θ.
t
Y para hallar el valor y el signo de la posición a
lo largo del eje y debemos aplicar la ecuación.
H o Y= Vo.t – g.t2/2.
O sea H o Y= Vo sen θ. t – g.t2/2
Ejercicio:
Una persona lanza oblicuamente una pelota con una velocidad inicial Vo = 10 m/s y un ángulo de lanzamiento θ = 60º. Suponga que la gravedad = 10 m/s2, desprecie la resistencia del aire y considere el momento del lanzamiento como el origen del conteo del tiempo (t=0).
a) En el
instante t = 0,50 s, ¿cuál es el valor de la velocidad de la pelota?
Como sabemos,
la pelota describirá una parábola (movimiento de un proyectil) y su velocidad
podrá obtenerse si conocemos sus componentes
v
x
Tenemos entonces:
x
Vx = Vo ∙cosθ
= 10∙cos60º = 10∙0,5= 5 m/s
⃗
v
y
Vy = Vo∙ senθ - g∙t = 10∙sen60º - 10∙0,5 = 10∙0,87 - 5 = 3,6
m/s
Observe que,
siendo
⃗
v
y
Vy >
0, podemos llegar a la conclusión de que la pelota, en ese instante, está desplazándose
hacia arriba, como se había establecido anteriormente. La magnitud de la
velocidad de la pelota, en ese instante será: V = √(Vx ^2 + Vy ^2 ) = √ (5,0^2+3,6^2) = √25 + 12,96 = √37,96 = 6,1 m/s
La posición
de la pelota, como vimos la proporcionan las coordenadas X e Y en donde la
pelota se
encuentra en
ese instante. Designando la posición de la pelota con el punto A, tenemos:
X = Vo x cosθ∙t =
10∙cos60º∙0,50= 2,5 m
Y = Vo x senθ∙t - 1/2∙g∙t
Y = 10∙sen60º∙0,5 – 1/2∙10∙0,50
Y = 3,1 m
1.
Consultar el
tutorial de you tube para reforzar.
DESEMPEÑO
FINAL:
Actividad a desarrollar:
Taller, teniendo como base el material entregado.
Resuelve el
siguiente problema:
Cualquier duda o inquietud,
enviar un mensaje al correo:
Ulisesdelarosa2010@gmail.com. Con gusto los atenderé.
Una vez terminado el taller final enviarlo a este correo. Plazo de envio de
actividades y talleres 24 de abril. 2020.
|
Con la supervisión y apoyo de los padres el
estudiante contestara el siguiente cuestionario.
Manejo del
recurso físico, textos y recursos informáticos para aclarar dudas con
el apoyo del cuidador o padres si es posible.
Se evaluará la comprensión de conceptos y la
solución de problemas.
|
Medios electrónicos,
taller, cuaderno, lápices, regla y borrador.
|
3. OBSERVACIONES:
ELABORADO POR:
Ulises De la Rosa Castrillón.
|
REVISADO POR:
|
Área:
Matemáticas
|
Asignatura:
Trigonometría.
|
|
Grado: 10°
|
Periodo:
II
|
|
Docente:
Ulises De la Rosa Castrillón.
Taller
No 1.
|
Duración:
3 horas .1 semana
|
Fecha: 26 de marzo. 2020.
|
2.
PLANEACIÓN:
ESTANDARES: Utiliza las propiedades
de los números reales para justificar procedimientos y diferentes
representaciones de subconjuntos de ellos.
|
||
Competencia del área: Comunicación,
Razonamiento y Solución de problemas.
|
||
DBA: Utiliza las propiedades de los
números reales para justificar procedimientos y diferentes representaciones
de subconjuntos de ellos.
|
||
TÓPICO GENERATIVO: Cuando
calculamos el volumen de un tanque utilizamos los números irracionales.
|
||
TÓPICO: Números reales: Números
irracionales (representación geométrica y ubicación en la recta numérica).
(DBA)
|
||
META DE COMPRENSIÓN: Los estudiantes
comprenderán como reconocer las características de los distintos conjuntos
numéricos, al utilizar el lenguaje matemático en la solución de situaciones
en diferentes contextos.
|
||
Desempeños de
comprensión
|
Valoración Continua (formativa)
|
Materiales y Recurso
|
DESEMPEÑO INICIAL: (Conocimientos
Previos)
Los
estudiantes responderán el siguiente cuestionario. Consultando la libreta,
libros de matemáticas y tutoriales en you tube.
Escribe frente a cada número a que conjunto
pertenece:
-4/7 (
), 5π ( ),
-28( ), √2
( ), 0,452 (
), 52 ( ),
-5, 37777… ( )
35 (
), 8,624624….. ( ) y 5/3 ( ).
Luego enviar al
correo que esta al final el documento con las respuestas, anotando el nombre
del estudiante.
El estudiante leerá el tópico generativo.
DESEMPEÑO
DE INVESTIGACIÓN GUIADA:
Se entregarán a los estudiantes el material
didáctico, el cual leerán y con la ayuda del video tutorial puede aclarar
dudas.
La unión del conjunto de los
números racionales con el conjunto de los números irracionales recibe el
nombre de conjunto de los números reales, y se denota con el
símbolo: R. El conjunto de
los números reales está formado por una serie de subconjuntos de números que
definiremos a continuación:
- Los números naturales que
surgen con la necesidad de contar
N = {1, 2, 3, 4, ...}
- Los números enteros que complementan a
los naturales pues contienen a los negativos y el cero.
- El conjunto de los Números
Racionales (Q) que
corresponden a la unión de todos los números cuya expresión
decimal es finita, infinita periódica o infinita
semiperiódica. Es decir, el conjunto de los números racionales está
compuesto por todos los números que pueden ser escritos como una fracción
cuyo numerador y denominador (distinto de cero) son números enteros.
Ejemplo:
- El conjunto de los Números
Irracionales (I) que está formado por la unión de todos
los números que admiten una expresión infinita no periódica.

Puesto que los naturales están
incluidos en los enteros y todos los enteros pueden ser
representados como un número racional, se dice que los números
reales son la unión de los números racionales y los irracionales.
Trazaremos tres números irracionales, que son la
raíz cuadrada de (2), la raíz cuadrada de (3) y la de (5). Debemos dibujar la
recta numérica de forma horizontal, y en el punto medio cero (0) hay que
dibujar una línea vertical. Marcamos dos unidades a la derecha y a la
izquierda en la línea horizontal, y dos unidades debajo y arriba de la misma,
sobre la línea vertical.
 
Hipotenusa = Raíz cuadrada de a al cuadrado más b
al cuadrado, si a horizontal es 1 y b vertical es 1. Si a al cuadrado es 1x1=
1 y b al cuadrado es 1x1 = 1 y los sumamos obtenemos 2 y si le sacamos la
raíz nos da √2.

Ahora trazaremos √3, ubicando
en el eje horizontal √2 y en el vertical 1, si trazamos una recta desde el
origen o cero hasta el punto vertical de 1 sobre la posición de √2, obtenemos
la hipotenusa que es √3.
Mirar en la gráfica siguiente como se utiliza el
teorema de Pitágoras donde a= √2 y b= 1.
Consultar
el sitio web. Para reforzar los conocimientos.
DESEMPEÑO
FINAL: Actividad a
desarrollar: Taller, teniendo como base el material entregado y el tutorial. Ubicar
en la recta numérica utilizando una hoja de papel milímetro, los siguientes
números irracionales:
a) √5 con eje horizontal 2 y eje vertical 1
b) √6 con eje
horizontal √5 y eje vertical 1
c) √7 con eje
horizontal √6 y eje vertical 1
d) √8 con eje
horizontal √7 y eje vertical 1.
Cualquier duda o inquietud,
enviar un mensaje al correo:
Ulisesegundo15@gmail.com. Con gusto los atenderé.
Una vez terminado el taller final enviarlo a este correo. Plazo de envio de
actividades y talleres 24 de abril. 2020.
|
Con la supervisión y apoyo de los padres el
estudiante contestara el siguiente cuestionario.
Manejo del
recurso físico, textos y recursos informáticos para aclarar dudas con
el apoyo del cuidador o padres si es posible.
Comprensión de conceptos.
Se evaluará la comprensión de conceptos y la
solución de problemas.
|
Medios electrónicos,
taller, cuaderno, lápices, regla y borrador.
|
3. OBSERVACIONES:
ELABORADO POR:
|
REVISADO POR:
|
Ulises De la rosa Castrillón.
|
Área:
Matemáticas
|
Asignatura:
Trigonometría.
|
|
Grado:
10°
|
Periodo:
II
|
|
Docente:
Ulises De la Rosa Castrillón.
Taller
No 2.
|
Duración:
3 horas .1 semana
|
Fecha: 26 de marzo. 2020.
|
2.
PLANEACIÓN:
ESTANDARES: Diseño estrategias para abordar
situaciones de medición que requieran grados de precisión específicos.
|
||
Competencia del área: Comunicación,
Razonamiento y Solución de problemas.
|
||
TÓPICO GENERATIVO: Sabias
que un aspersor es un dispositivo mecánico que gira sobre un mecanismo que le
produce un sexto de rotación y se usa para el riego de césped o cultivos.
|
||
TÓPICO: Sistemas de medición
angular:
·
Ángulos.
·
Sistemas
de medición angular.
|
||
META DE COMPRENSIÓN: Los estudiantes
comprenderán las principales características de los sistemas de medición
angular y cómo realizar conversiones de medidas de ángulos a través de las
equivalencias entre grado y radián
para aplicarlos en la solución de situaciones problemas.
|
||
Desempeños de
comprensión
|
Valoración Continua (formativa)
|
Materiales y Recurso
|
DESEMPEÑO INICIAL: (Conocimientos
Previos)
Los estudiantes
responderán el siguiente cuestionario. Consultando la libreta, libros de
matemáticas y tutoriales en you tube.
Resuelve la siguiente pregunta y actividad:
1.- ¿Qué ángulo forman las manecillas del reloj a
las 2:00, 3:00, 4:00, 6:00, 8:00, 9:00, 8:00, 10:00 y a las 12?
2.- Realiza dos dibujos en el primero ubica los
ángulos de las: 3,6,9 y 12 horas y en el segundo 2,4,8 y 10 horas.
Luego enviar al
correo que esta al final el documento con las respuestas, anotando el nombre
del estudiante.
El estudiante leerá el tópico generativo.
DESEMPEÑO
DE INVESTIGACIÓN GUIADA:
Se entregarán a los estudiantes el material
didáctico, el cual leerán y con la ayuda del video tutorial puede aclarar
dudas.
SISTEMA SEXAGESIMAL DE MEDICIÓN
ANGULAR.
La medida del ángulo de giro de la brújula esta
expresada en el sistema sexagesimal. En este sistema, un ángulo de rotación
completa se divide en 360 ángulos iguales. Cada ángulo mide un grado 1°
sexagesimal. Para medir ángulos más pequeños se utilizan los minutos (´) y
los segundos (“). Si 1° se divide en 60 ángulos iguales, cada uno de ellos
equivale a 1´; y si 1´ se divide en 60 ángulos iguales, cada uno de ellos
equivale a 1”. Ejemplo: una medida puede ser expresada en 52 grados, 24
minutos y 18 segundos. 52° 24´ 18”.
En el sistema sexagesimal se manejan las siguientes
equivalencias:
1° = (1/360) °
1´ = (1/60) ° 1” = (1/3600)
° 1° = 60´ 1´ = 60”.
Ejemplo 1. Determina la expresión decimal de la
medida 52° 24´ 18”.
52° + 24´x (1/60) ° + 18”x (1/3600) ° = 52° + 0,4°
+ 0,005°, donde:
24x1= 24entre 60 = 0,4 y 18x1 = 18entre 3600 =
0,005.
Si sumamos las tres cifras, tenemos que: 52° 24´ 18” = 52,405°
Grados sexagesimales y radianes. Qué son los
radianes
Para medir los ángulos se pueden
utilizar dos unidades: los grados sexagesimales y los radianes. Ambas
unidades son equivalentes
¿Y qué significa que sean
equivalentes?
Pues que, para el mismo ángulo,
su valor lo puedes dar en ángulos o en radianes y por tanto se puede
convertir de una unidad a otra.
Normalmente, estamos más familiarizados
con los grados, ya que es lo primer que nos enseñan. Como ya sabes, una
vuelta completa de circunferencia tiene 360º:
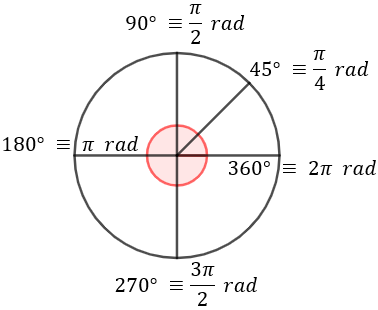
Esos mismos ángulos también se pueden medir en radianes. Una
circunferencia tiene 2π radianes:
Un ángulo recto tiene π/2 radianes y una
semicircunferencia de 180 °, mide π radianes:
La
equivalencia entre grados y radianes es la siguiente:
¿cuántos radianes son 60º?
Planteamos la regla de tres:
Si 180º son.......... 1π radianes
60º serán........... x radianes.
Ponemos los grados debajo de los grados
y los radianes debajo de los radianes:
Ya sólo nos queda
multiplicar en cruz. Para dejar el resultado en múltiplos de π, simplificamos (sacamos mitad y tercera) a los números que tenemos
en la operación y nos queda:
Y ahora despejamos la x: X = 60°x 1
Por tanto, 60º
equivalen a π /3 radianes:
Para pasar de radianes
a grados, lo hacemos igual que antes, con una regla de 3, solo que esta vez,
la incógnita a despejar serán los grados.
¿Cuántos grados son 3π /4 radianes?
Planteamos la regla de tres:
Si 1π radianes son..........180º
3π/4
radianes serán....... x grados:
Despejamos la x
y resolvemos: X = 180° x
Por tanto, 3π/4
radianes equivalen a 135º
Consultar el sitio web. Para reforzar los
conocimientos. https://www.youtube.com/watch?v=326Jj4OKHaQ
DESEMPEÑO
FINAL: Actividad a
desarrollar: Taller, teniendo como base el material entregado y el tutorial.
1.- Convertir 72°, 120°,
108°, 144° y 300°
2.- Convertir 1/5π rad , 2/9π rad, 1/6π rad, 4/9π rad, 2/3π rad.
Cualquier duda o inquietud,
enviar un mensaje al correo:
Ulisesegundo15@gmail.com. Con gusto los atenderé.
Una vez terminado el taller final enviarlo a este correo. Plazo de envío de
actividades y talleres 24 de abril. 2020.
|
Con la supervisión y apoyo de los padres el estudiante contestara el siguiente cuestionario.
Manejo del
recurso físico, textos y recursos informáticos para aclarar dudas con
el apoyo del cuidador o padres si es posible.
Comprensión de conceptos.
Se evaluará la comprensión de conceptos y la
solución de problemas.
|
Medios electrónicos,
taller, cuaderno, lápices, regla y borrador.
|
Comentarios
Publicar un comentario